经验百科
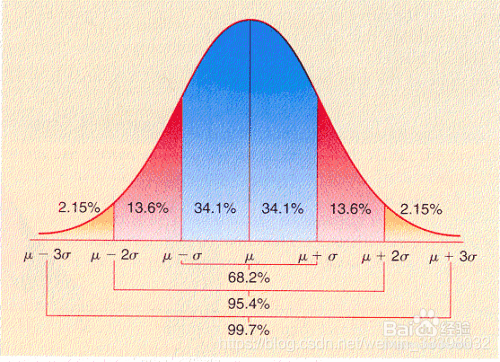
在实验科学中有对应正态分布的3σ定律，是一个简单的推论，内容是：“几乎所有”的值都在平均值正负三个标准差的范围内，也就是在实验上可以将99%的几率视为“几乎一定”。
不过上述推论是否有效，会视探讨领域中“显著”的定义而定，在不同领域，“显著”的定义也随着不同。
例如在社会科学中，若置信区间是在正负二个标准差（95%）的范围，即可视为显著。但是在安全要求较高的行业中，置信区间要到正负三个标准差（99%）的程度，即3σ定律。
该定律在统计学中以假设检验的方式，得到广泛应用。
工具/原料
- Minitab
方法/步骤
假设某工厂生产了一批钢梁，质量经理想确认该批钢梁长度的平均值大于420cm.
抽样测量钢梁的长度并记录。
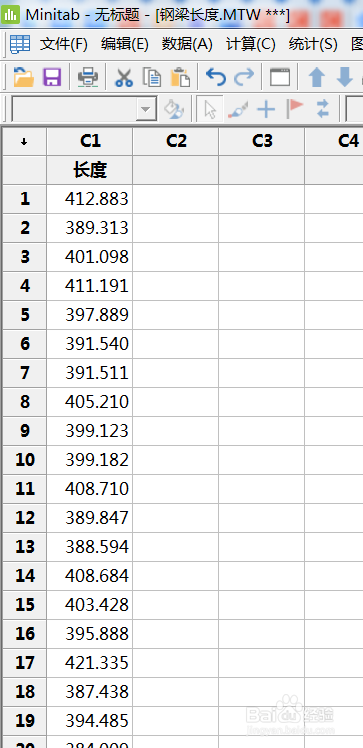
测试钢梁的长度数据符合正太分布。p>0.05,符合正太分布
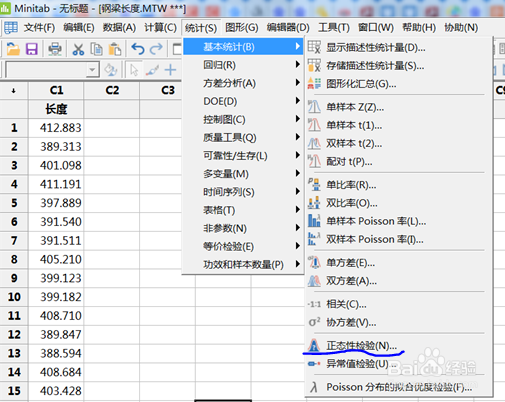
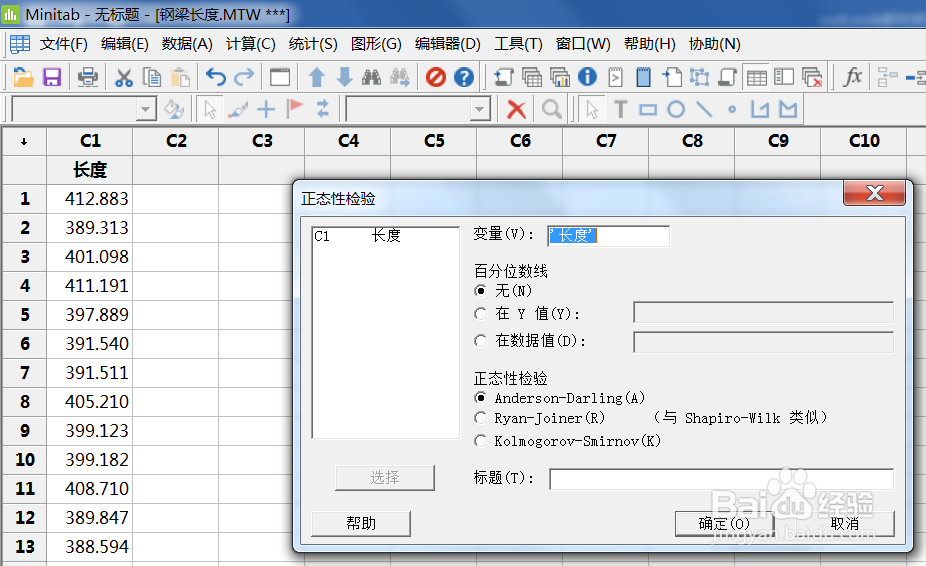
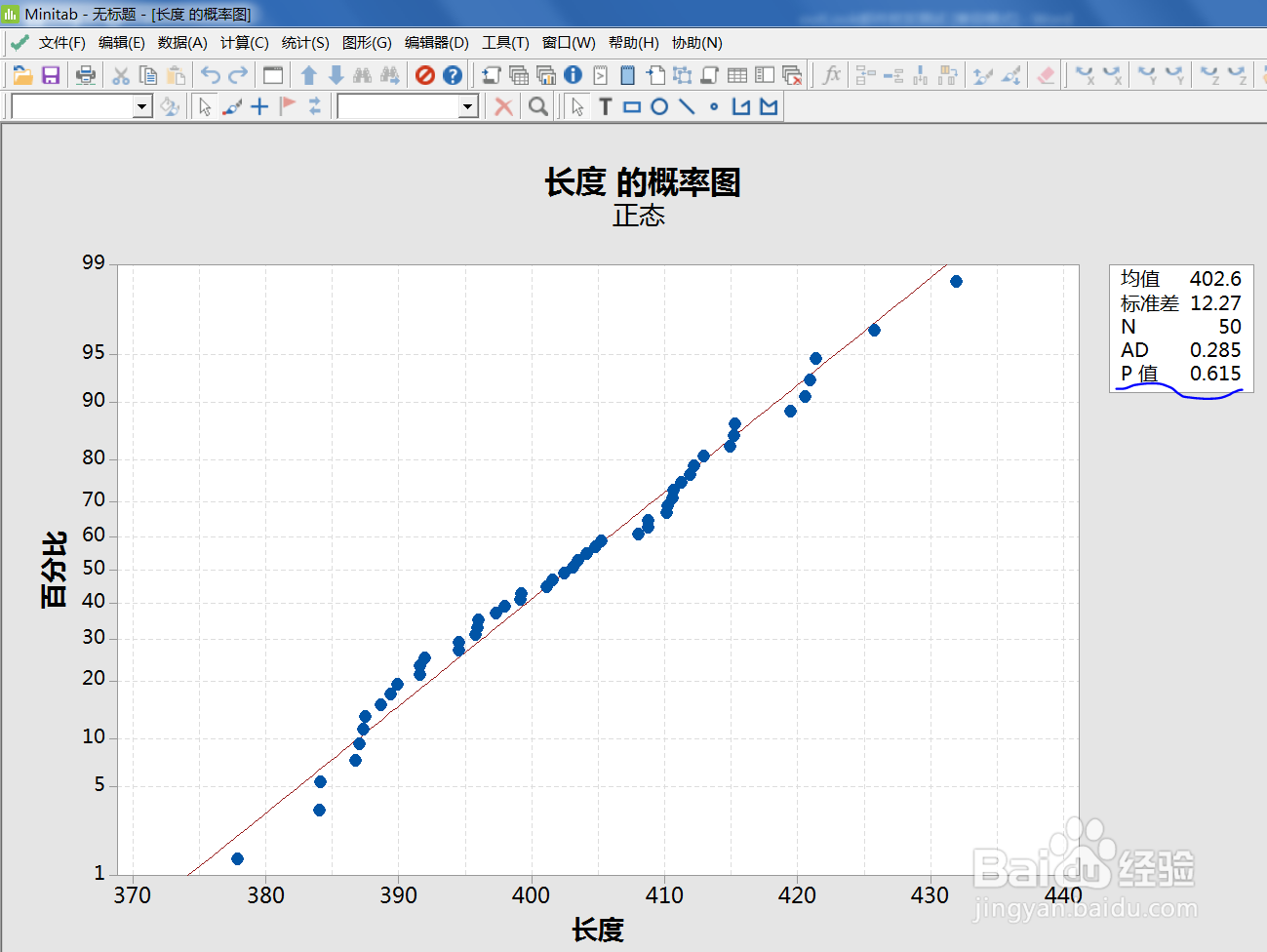
建立假设：
Ho: 均值u=420
H1:均值u>420
利用协作进行假设检验。显著性水平选择0.01.
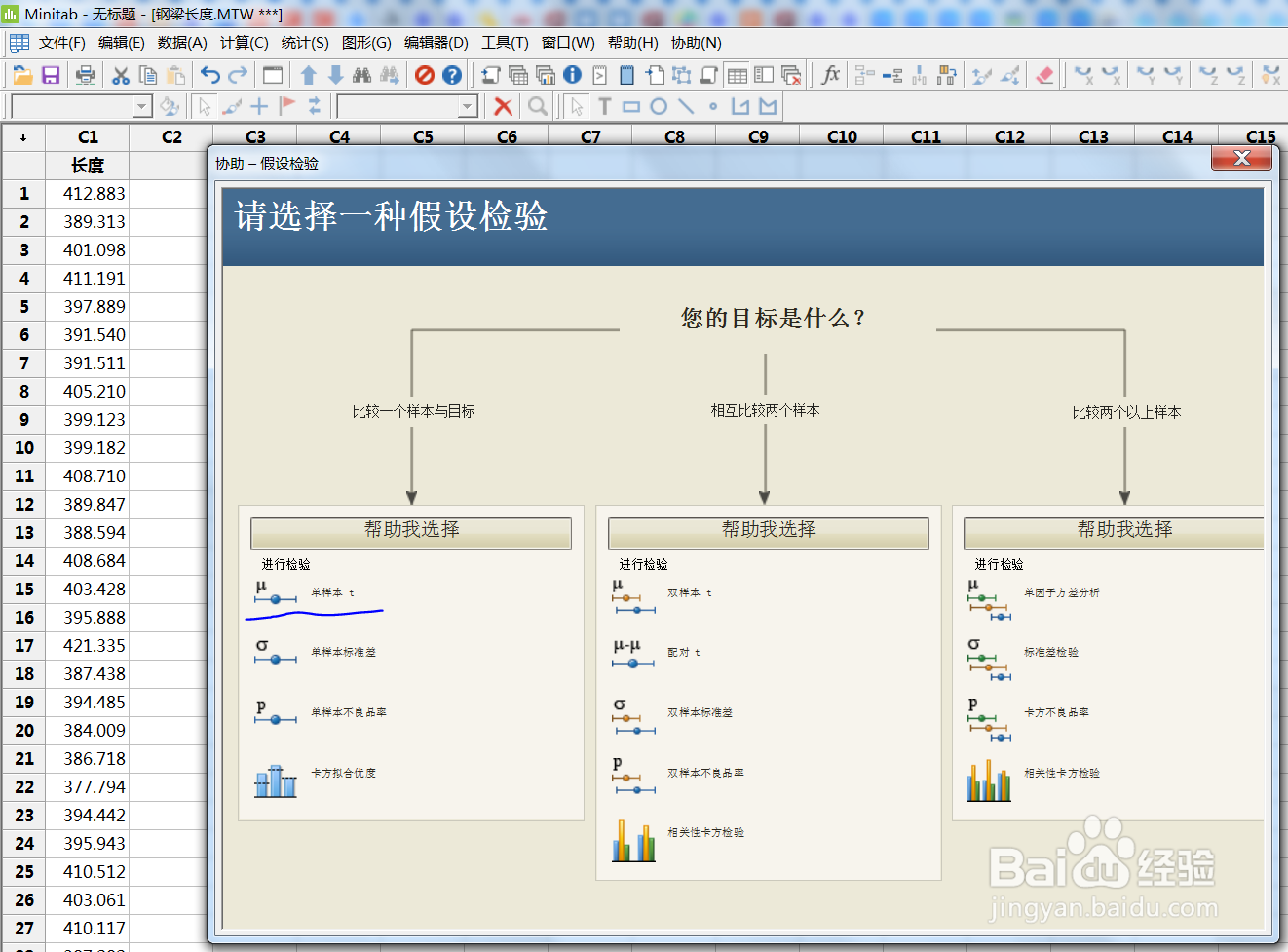
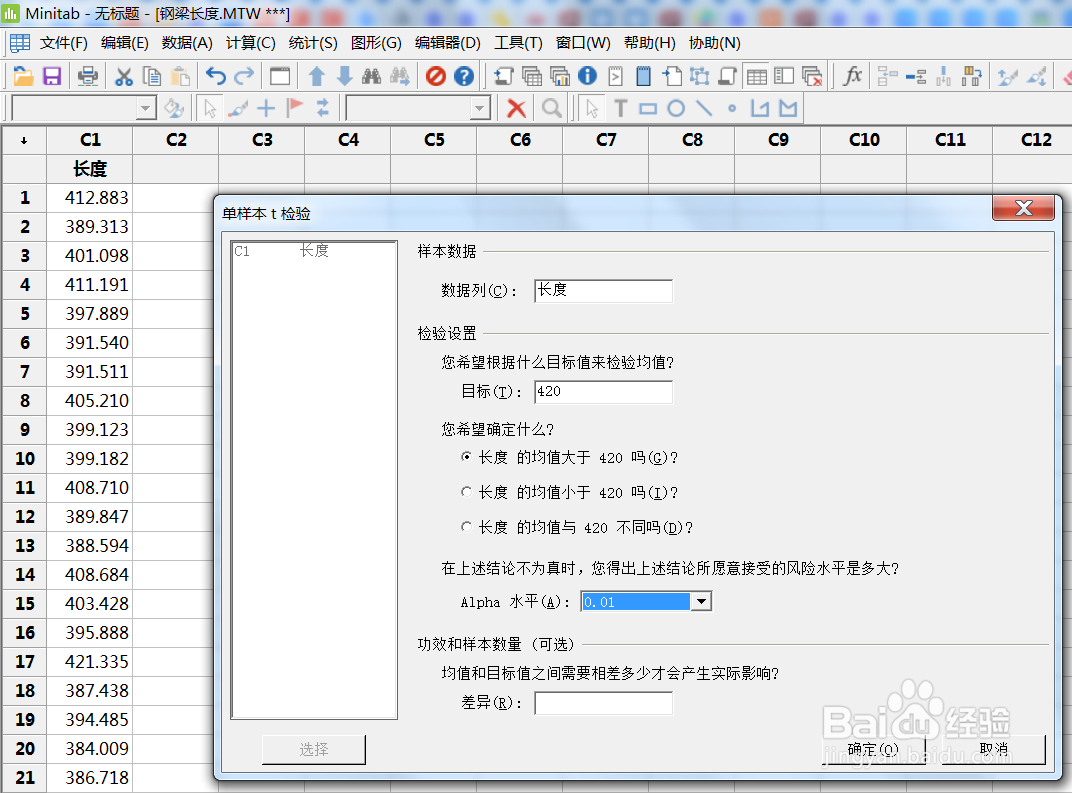
p>0.01,所以不能拒绝H0假设。不能证明钢梁长度大于420cm.
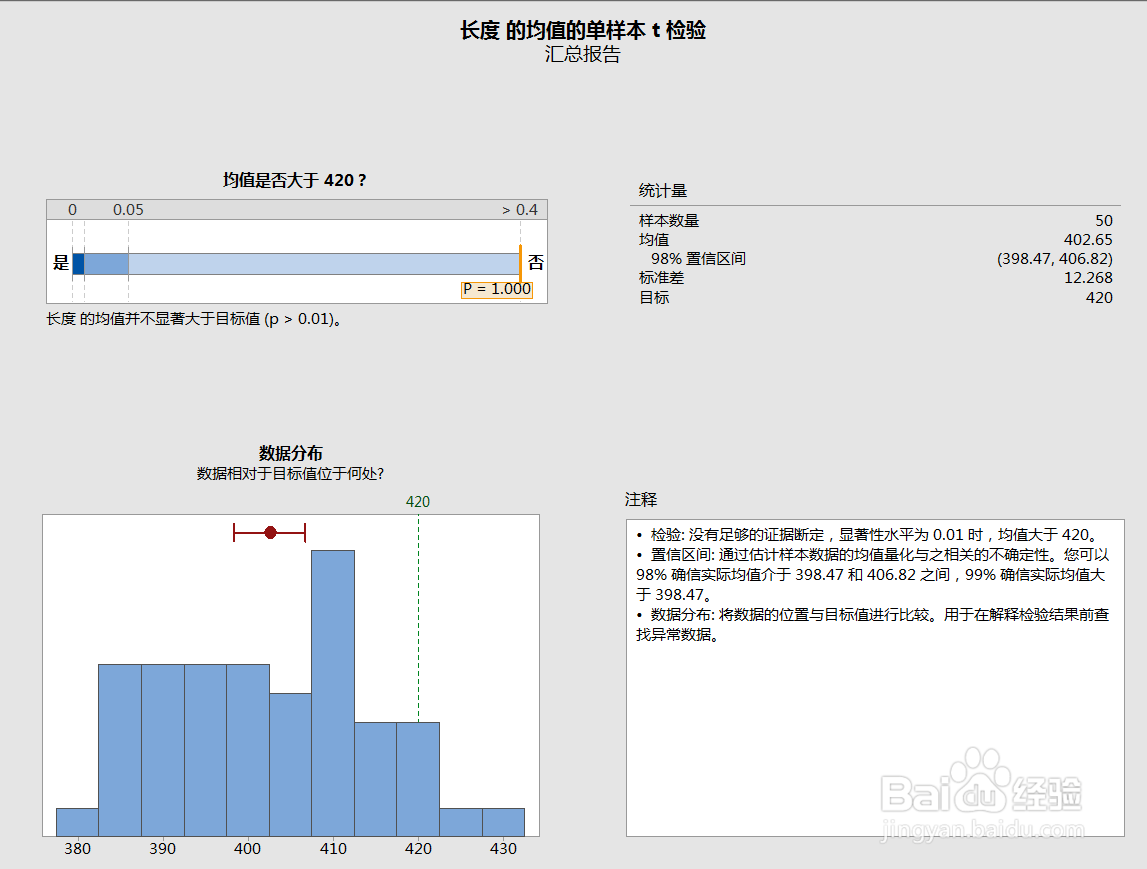
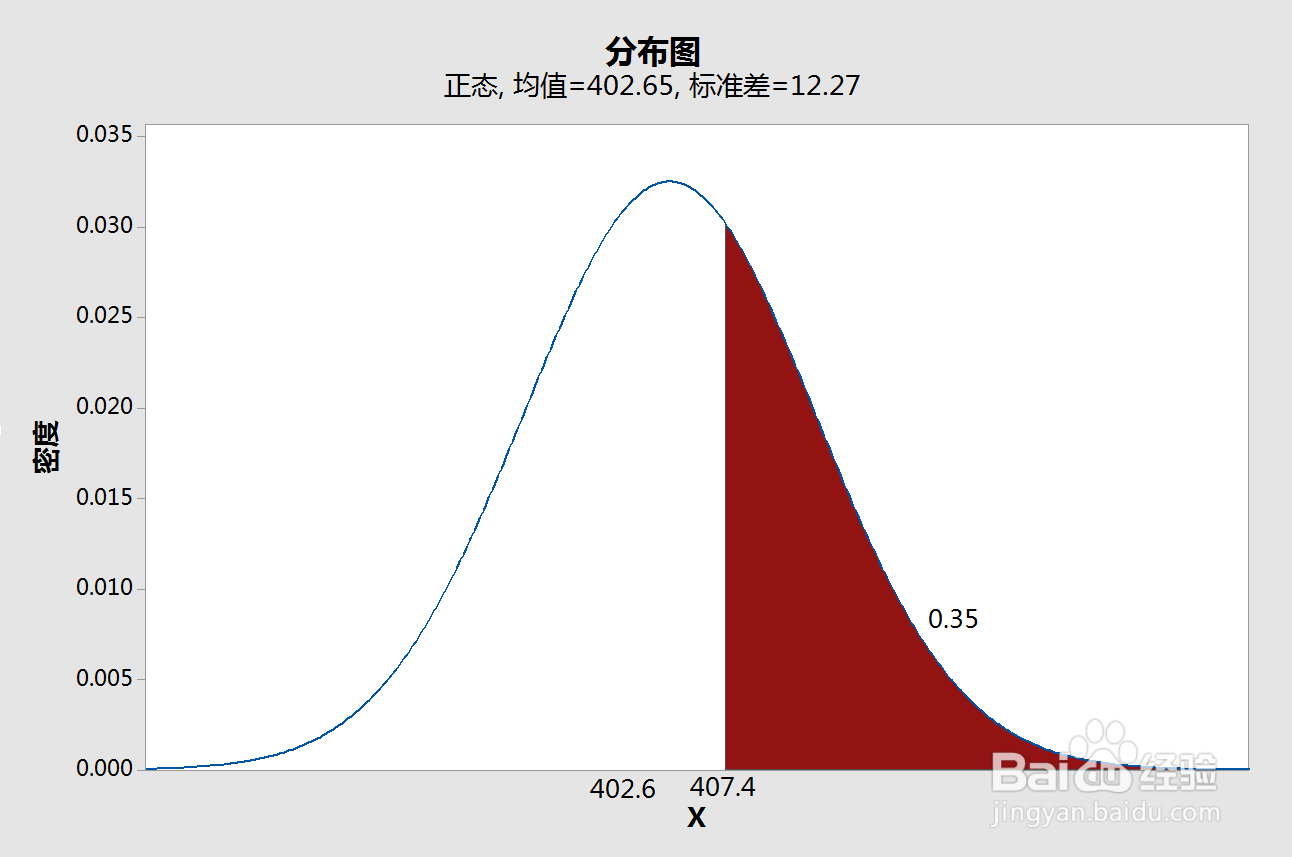
下面我们分别看一下，显著性水平分别选择1σ、2σ、3σ，对应的接受H1假设的取样均值的临界值分别为407.4、422.8、431.2。
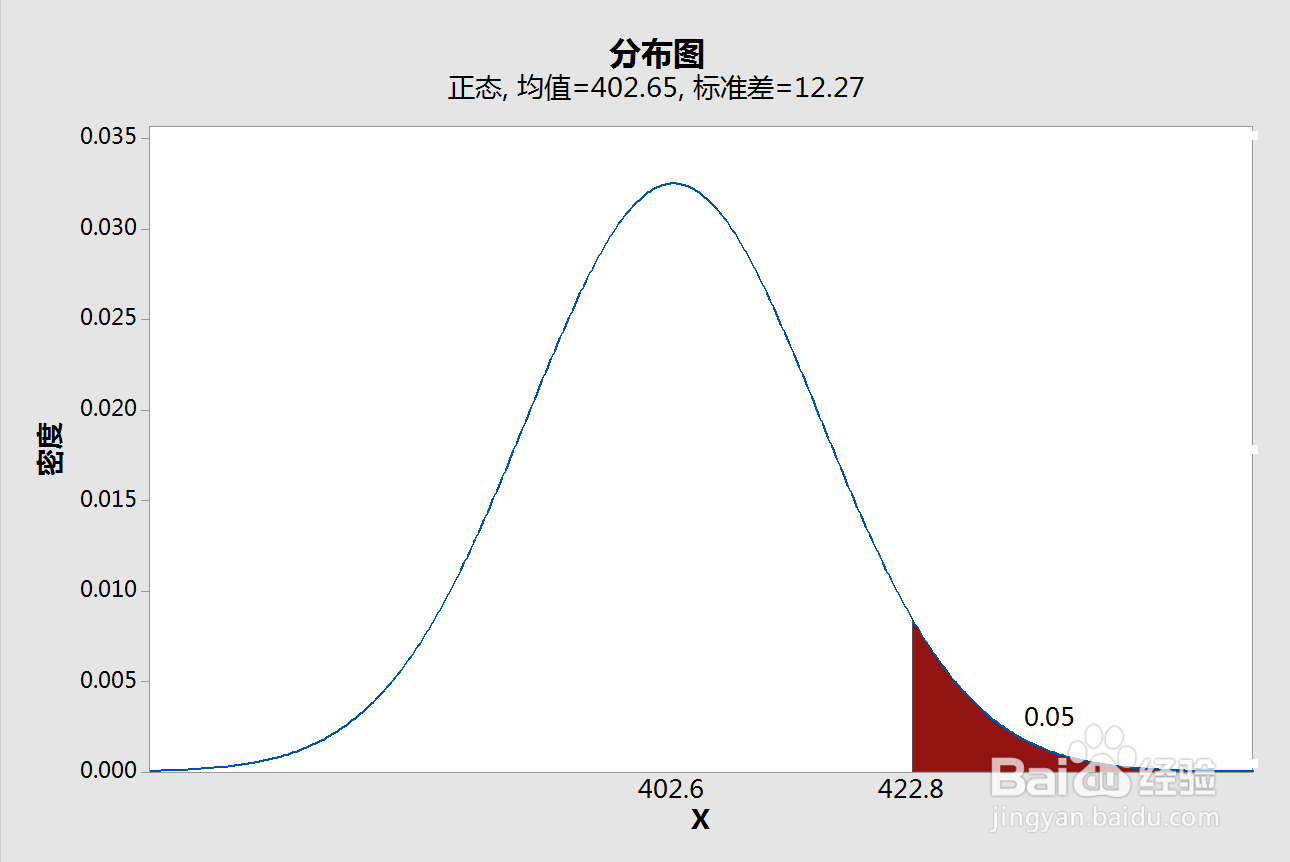
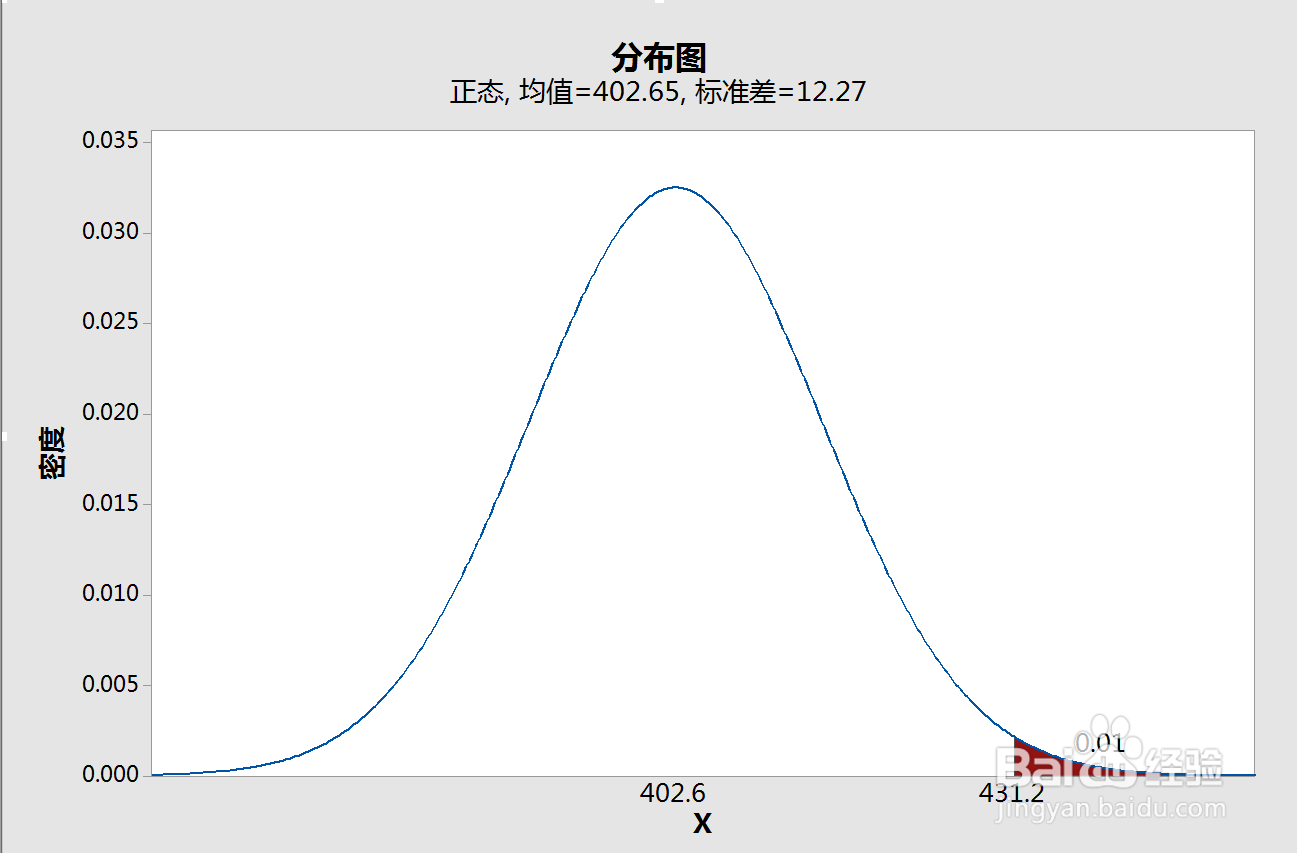END
未经允许不得转载：经验百科 » 正态分布3σ原则怎么用
最新评论
好东西