经验百科本经验通过函数的定义域、单调性、凸凹性、奇偶性等性质，介绍函数用导数工具画函数y=ln(11/24+40x^2/83)的图像的主要步骤。
解析函数的定义域，结合对数函数的性质，要求真数为正数，即可求解函数的定义域。
解析函数的单调性，计算函数的一阶导数，得到函数的驻点，进而求出函数的单调区间。
函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时，函数值f(x)也随着增大(或减小)，则称该函数为在该区间上具有单调性。
通过函数的二阶导数，计算函数的拐点，进而计算函数的凸凹区间。
如果函数f(x)在区间I上二阶可导，则f(x)在区间I上是凸函数的充要条件是f''(x)<=0。
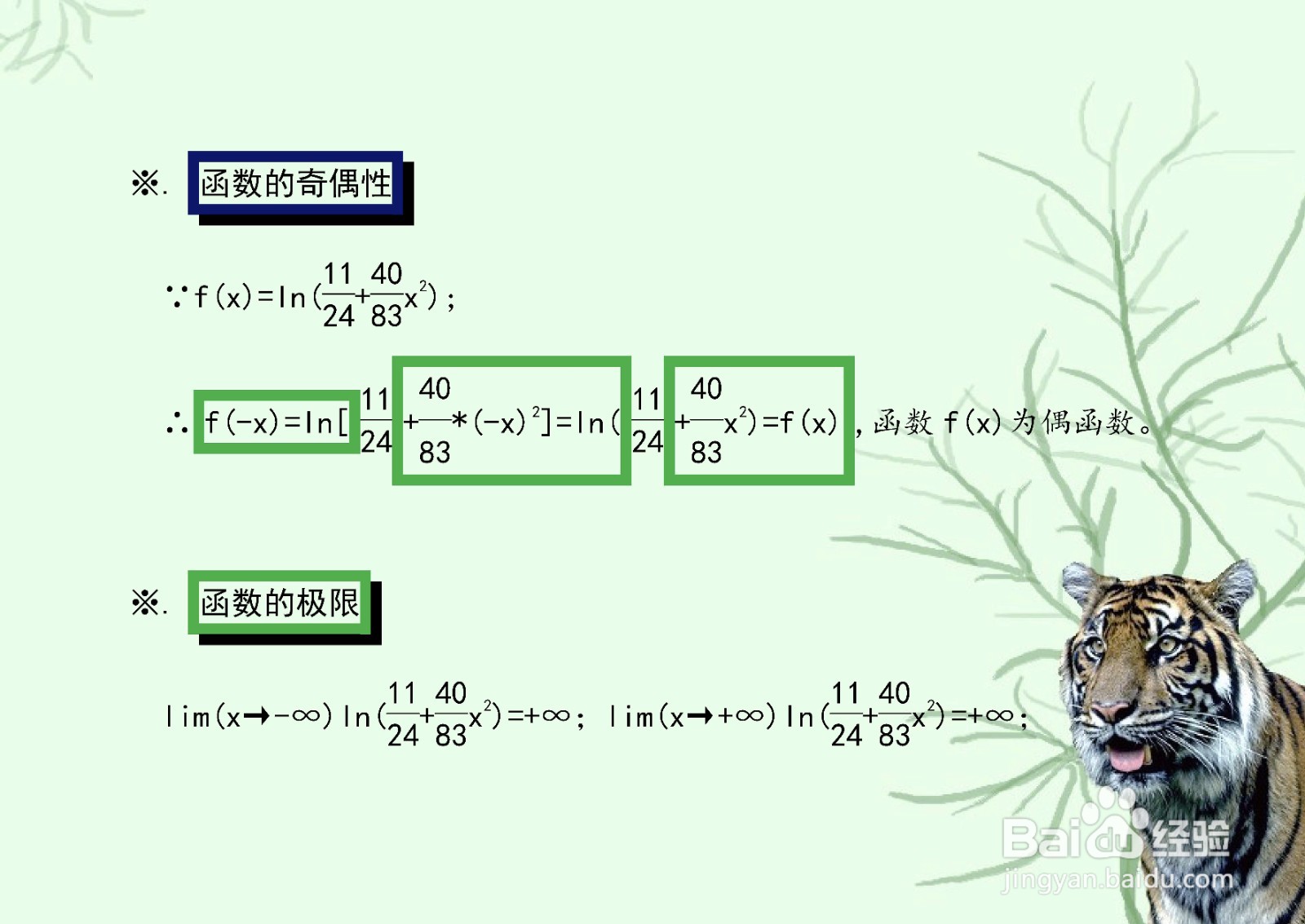
由函数奇偶性判断原则，可判断函数为偶函数，图像关于y轴对称，并计算函数的极限。
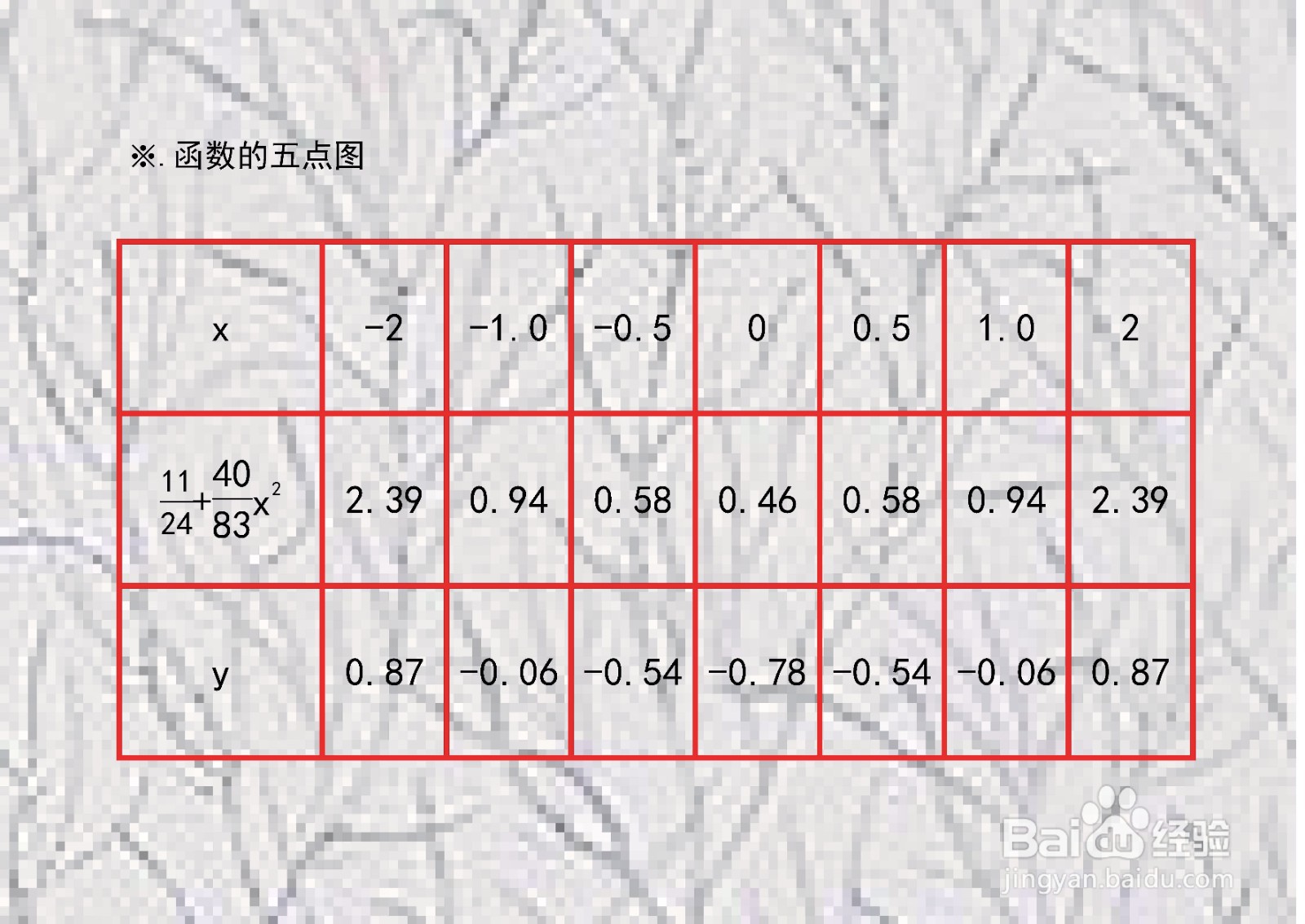
函数上的五点图列表如下。
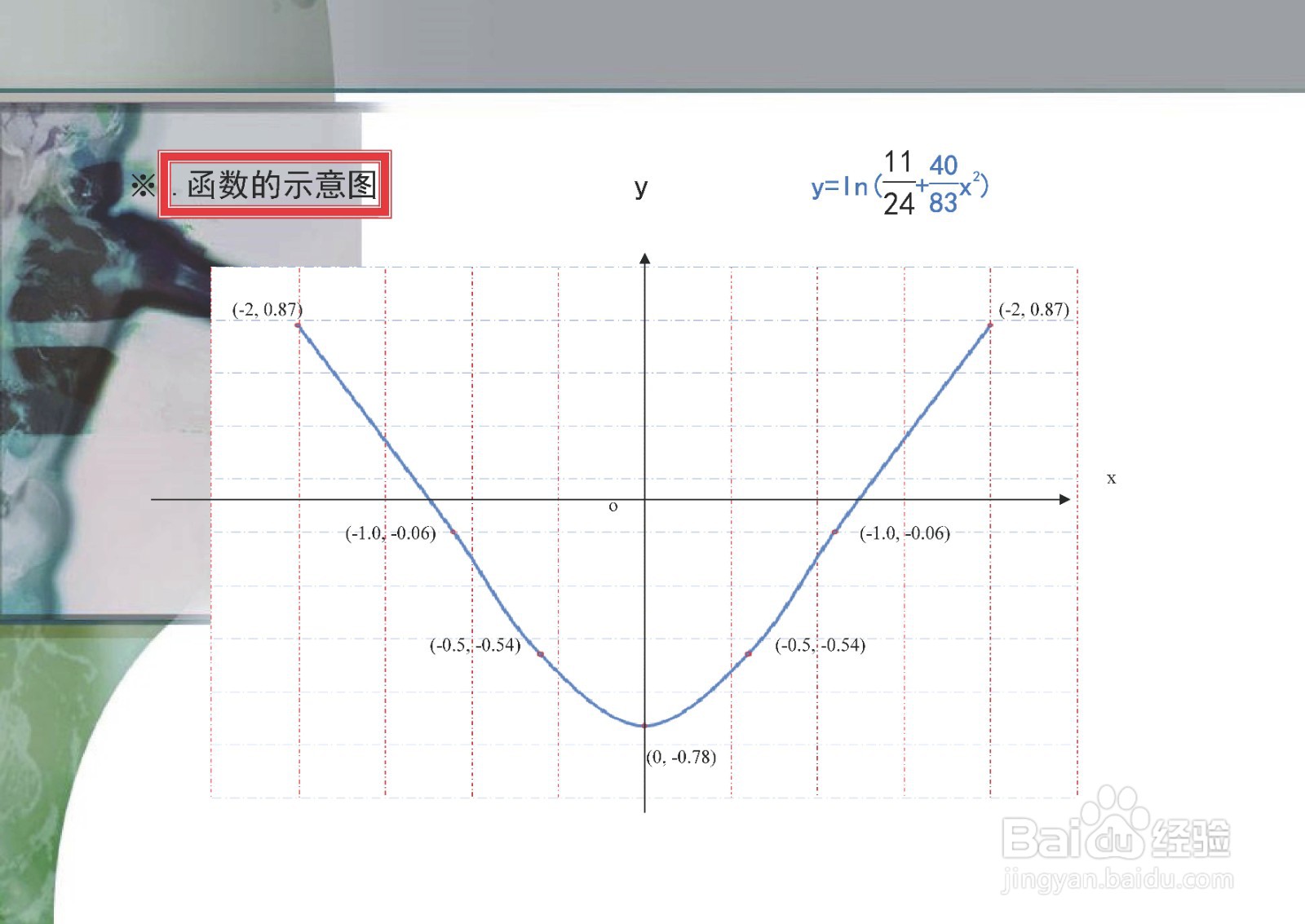
根据以上函数的定义域、单调性、凸凹、极限和奇偶等性质，并结合函数的驻点和拐点，即可画出函数的示意图如下。
END未经允许不得转载：经验百科 » 函数y=ln(11/24+40x^2/83)的图像示意图怎么画？
推荐给朋友的视频，可在主页推荐列表中查看。下面将介绍抖音APP如何查看推荐给朋友的视频。工具/原料vivox80OriginOS 3.0抖音27.7方法/步骤进入抖音APP首页，点击底部“我”选...
阅读(0)评论(0)
别人夸你帅怎么幽默回答方法/步骤1、幽默一点 首先，最机智的回复就是幽默一点的回复，以调侃的方式回复，比如我们可以回复“我就喜欢你这样一本正经胡说八道的人”，这种调侃的...
阅读(0)评论(0)
如下：1、隔窗闻漫雪，咫尺若天涯。2、真情到久难相见，相约梦中总是缘，千杯万盏终恨少，不觉梦醒晓风寒。3、众里寻他千百度，蓦然回首，那人却在，灯火阑珊处。4、既然不能在一起，生命为什...
阅读(0)评论(0)
关闭个性化推荐功能，即可关闭直播推荐，下面将介绍具体的设置方法。工具/原料小米13MIUI14.0汽水音乐7.8.0方法/步骤打开APP我的页，点击右上角“设置”图标。进入设置页，点击“隐...
阅读(0)评论(0)
对方说上班了，怎么回消息 方法/步骤首先对方和你说上班了，第一个意思是告诉你他的状态在忙，这时候你可以表示理解说：你先忙着，我就不打扰你啦。这可以表达出你的体贴，还很善解人意...
阅读(0)评论(0)
如果男生给你说七夕节快乐该怎么回答呢？方法/步骤假如你是一个女生，一个男生给你说七夕节快乐的话。那么他可能是想看看你有没有男朋友呢？假如你已经有了对象他给你发的话，那么...
阅读(0)评论(0)
下面将介绍快手极速版静音模式怎么设置。工具/原料红米Note12MIUI14.0快手极速版11.9.40方法/步骤打开快手极速版app，在个人主页点击“三个点”图标。在更多页，点击“设置”图...
阅读(0)评论(0)
人家发消息说句七夕快乐，怎么回复对方工具/原料微信，QQ或短信方法/步骤如果对方并不是你喜欢的类型，你可以回答说：嗯，谢谢你，祝福你。如果一个男生给你说七夕快乐，说明他是对你有好...
阅读(0)评论(0)
最新评论
好东西